Template abstract class, mother class for tetraedrons and facettes. More...
#include <element.h>
Public Member Functions | |
| element (const std::vector< Nodes::Node > &_p_node, const int _idx, std::initializer_list< int > &_i) | |
| constexpr int | getN (void) const |
| constexpr int | getNPI (void) const |
| void | buildMatP (Eigen::Ref< Eigen::Matrix< double, 2 *N, 3 *N >> P) |
| virtual void | getPtGauss (Eigen::Ref< Eigen::Matrix< double, Nodes::DIM, NPI >> result) const =0 |
| void | infos (void) |
Public Attributes | |
| std::vector< int > | ind |
| int | idxPrm |
| Eigen::Matrix< double, NPI, 1 > | weight |
| Eigen::Matrix< double, 2 *N, 2 *N > | Kp |
| Eigen::Matrix< double, 2 *N, 1 > | Lp |
Protected Member Functions | |
| const Nodes::Node & | getNode (const int i) const |
| bool | existNodes (void) const |
| void | zeroBasing (void) |
Private Member Functions | |
| virtual void | orientate ()=0 |
Private Attributes | |
| const std::vector< Nodes::Node > & | refNode |
Detailed Description
template<int N, int NPI>
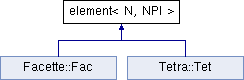
class element< N, NPI >
Template abstract class, mother class for tetraedrons and facettes.
template parameters are N number of sommits and NPI number of interpolation points. It contains a list of indices to the N nodes of the element, a reference to the full nodes vector, and index refering to the associated material parameters. All indices are zero based, derived class constructor should call zerobasing() if needed. It contains also the vector and matrix weight, Kp, Lp, P related to finite element computations. weight values are not initialized, they have to be set by derived class constructor. Member function getPtGauss() returns Gauss points. orientate() is a pure virtual function, it should manipulate indices to orientate positively the element.
Constructor & Destructor Documentation
◆ element()
|
inlineexplicit |
constructor
- Parameters
-
_p_node vector of nodes _idx index to params _i indices to the nodes
Member Function Documentation
◆ buildMatP()
|
inline |
build matrix P direcly from ep,eq in nodes P is block diagonal: ( Epx Epy Epz ) ( Eqz Eqy Eqz ) with each block E(p|q)(x|y|z) a N*N diagonal matrix see here http://eigen.tuxfamily.org/dox-devel/TopicTemplateKeyword.html for the wierd template syntax
- Parameters
-
[out] P block diagonal matrix
◆ existNodes()
|
inlineprotected |
returns true if mesh node vector is not empty
◆ getN()
|
inlineconstexpr |
getter for N
◆ getNode()
|
inlineprotected |
returns reference to node at ind[i] from mesh node vector
◆ getNPI()
|
inlineconstexpr |
getter for NPI
◆ getPtGauss()
|
pure virtual |
computes Gauss point of the element, return in result
Implemented in Tetra::Tet, and Facette::Fac.
◆ infos()
|
inline |
print the vector index of the associated region and the node indices of the element
◆ orientate()
|
privatepure virtual |
a method to orientate the element
Implemented in Tetra::Tet, and Facette::Fac.
◆ zeroBasing()
|
inlineprotected |
zeroBasing: index convention Matlab/msh (one based) -> C++ (zero based)
Member Data Documentation
◆ idxPrm
| int element< N, NPI >::idxPrm |
index of the material region of the element
◆ ind
| std::vector<int> element< N, NPI >::ind |
indices to the nodes
◆ Kp
| Eigen::Matrix<double,2*N,2*N> element< N, NPI >::Kp |
matrix for integrales
◆ Lp
| Eigen::Matrix<double,2*N,1> element< N, NPI >::Lp |
vector for integrales
◆ refNode
|
private |
vector of nodes
◆ weight
| Eigen::Matrix<double,NPI,1> element< N, NPI >::weight |
weights hat function of the element
The documentation for this class was generated from the following file: